服务热线
13430557816
在信号处理领域,原始信号往往伴随 “多源异构、量纲混乱、幅值失衡" 三大问题。例如某旋转机械监测系统,振动加速度传感器输出信号量纲为m/s²(幅值范围0.5~10),速度传感器为mm/s(幅值范围1~3),声压传感器为dB(幅值范围60~100)——若直接将这些数据输入故障诊断模型,模型会因 “大数值特征权重过高,小数值特征被忽略",导致分析结果失真。
数据标准化的核心目标,是在保留信号物理意义与变化趋势的前提下,消除量纲差异与幅值偏移,使不同类型、不同来源的信号特征处于统一尺度。尤其在振动信号处理(如旋转机械故障诊断)、声学信号分析(如设备噪声溯源)、生物医学信号(如心电信号)等场景中,标准化是衔接 “信号预处理" 与 “特征提取 / 模型诊断" 的关键桥梁,直接影响后续分析的精度与可靠性。
一、数据标准化的核心原理
信号数据的本质是 “随时间 / 空间变化的物理量",其标准化需兼顾 “统计特性" 与 “信号物理意义",区别于传统数据挖掘的通用标准化方法。如下聚焦信号处理中的Z-score 标准化(也称为均值 - 标准差标准化),展开技术细节。
1. 基础公式
Z-score标准化的核心是将原始信号数据x转换为均值为 0、标准差为 1 的分布,公式如下:
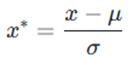
其中:
x为原始信号采样点(如振动信号某时刻的加速度值、温度信号某时刻的温度值);
μ为信号序列的均值(反映信号的 “基准水平",如正常设备振动的平均幅值);
σ为信号序列的标准差(反映信号的 “波动程度",如振动信号的幅值离散性);
x*为标准化后的信号值(消除量纲,可理解为 “偏离基准水平的标准差倍数")。
传统数据标准化中,μ与σ通常基于全量数据计算,但信号处理中需考虑信号的时序性与动态性,避免 “静态统计量导致的信息失真",核心差异如下:
信号特性 | 统计量计算方式 | 适用信号类型 | 工程案例 |
平稳信号(如电机稳态振动) | 全局统计量(全信号序列的μglobal、σglobal) | 频率成分固定、幅值波动小的信号(如额定转速下的轴承振动) | 某风机稳态运行时,振动信号10分钟序列的μ=0.8g,σ=0.15g,用全局 Z-score 标准化后,频谱分析的特征频率更清晰 |
非平稳信号(如电机启动过程) | 滑动窗口统计量(窗口内μwindow、σwindow) | 频率 / 幅值随时间变化的信号(如设备启停、负载切换) | 某电机启动过程(转速从 0 升至 1500rpm),用100ms滑动窗口计算μ与σ,标准化后避免 “启动初期小幅值信号被压缩" |
多段信号(如批次采集的振动数据) | 分段统计量(每段信号独立计算μsegment、σsegment) | 分批次采集、环境差异大的信号(如不同工况下的齿轮箱振动) | 某生产线 3 台相同电机的振动数据,因安装误差导致μ差异达0.5g,分段标准化后实现跨设备特征对比 |
3. 标准化与 “归一化" 的区别
信号处理中,标准化(Z-score)与归一化(如 Min-Max)常被混淆,但二者的适用场景因 “信号特性" 存在明确边界,具体对比如下:
对比维度 | Z-score 标准化 | Min-Max 归一化([0,1]区间) | 信号场景选择建议 |
核心逻辑 | 基于信号的统计分布调整 | 基于信号的极值范围压缩 | 若信号近似正态分布(如平稳振动),选标准化;若信号极值有明确物理意义(如声压级 0~120dB),选归一化 |
对异常值敏感性 | 敏感(异常值会拉高σ,导致标准化后幅值收缩) | 极敏感(异常值直接决定xmax/xmin,压缩正常数据) | 信号含少量脉冲噪声(如传感器磕碰)时,标准化比归一化更可靠,需先做异常值抑制再处理 |
物理意义保留 | 保留 “偏离基准的程度"(如正负值反映波动方向) | 仅保留 “相对大小"(丢失正负方向信息) | 振动加速度(含正负方向)、电流信号(正负半周)等需保留方向的信号,必须用标准化;温度、压力等非负信号可任选 |
模型适配性 | 适配对分布敏感的模型(SVM、逻辑回归、LSTM) | 适配需非负输入的模型(CNN 卷积层、自编码器) | 振动信号时序预测用 LSTM 时,标准化后梯度更新更稳定;时频图输入 CNN 时,Min-Max 归一化更适配像素值范围 |
在信号处理工程实践中,标准化常因 “忽略信号特性" 导致效果适得其反,以下梳理四类典型误区及应对策略。
问题描述:在信号分类 / 诊断模型训练中,直接用 “训练集 + 测试集" 的全量数据计算μ与σ,会使测试集的信息提前融入训练过程,导致模型泛化能力下降。
工程案例:某轴承故障诊断任务中,训练集(800 组)与测试集(200 组)混合计算μ=0.4g,σ=0.12 g,标准化后模型测试准确率达 98%;但分开计算时(训练集μ=0.38g,σ=0.11g,测试集用训练集统计量标准化),准确率降至 85%,暴露了数据泄露的虚假效果。
解决方案:严格遵循 “训练集统计量优先" 原则 —— 仅用训练集计算μtrain与σtrain,测试集、验证集均使用该统计量标准化,确保测试过程的独立性。
问题描述:信号中的毛刺(如传感器接触不良导致的 5 倍幅值跳变)会大幅拉高σ,使正常信号标准化后幅值收缩至接近 0,丢失有效信息。
工程案例:某风机振动信号含 1 个异常值(5g,正常范围0.2~0.8g),全量计算σ=0.6g,标准化后正常信号0.2g对应x*=(0.2-0.5)/0.6=-0.5,0.8g对应x*=-0.5,幅值差异被压缩 80%。
解决方案:标准化前行异常值处理:
用箱型图法([Q1-1.5IQR, Q3+1.5IQR])识别异常值;
对异常值用 “三次样条插值" 替换(保留信号平滑性);
再计算μ与σ,此时σ降至0.15 g,正常信号标准化后幅值差异恢复至[-2, 2],冲击特征清晰。
问题描述:部分信号的幅值本身具有明确物理意义(如声压级0dB为听觉阈值,120dB为痛阈),标准化后会丢失这些关键物理信息。
工程案例:某车间噪声监测中,将60~110dB的声压级标准化后,85dB(职业暴露限值)对应x*=0.5,现场人员无法通过标准化值直接判断是否超标。
解决方案:分场景选择是否标准化:
若后续为 “定量分析"(如是否超标、噪声源强度),保留原始信号,仅做量纲转换(如将Pa转换为dB);
若后续为 “定性诊断"(如噪声源类型识别),再进行标准化,且需记录原始统计量,便于结果回溯。
问题描述:多传感器(如振动 + 温度 + 电流)信号处理中,用同一组μ与σ标准化不同类型信号,导致物理意义冲突。
工程案例:某电机监测系统中,振动信号(μ=0.4g,σ=0.1g)与温度信号(μ=45℃,σ=5℃)混用统计量,标准化后温度55℃对应x*=(55-0.4)/0.1=546,掩盖振动信号的特征。
解决方案:多源信号采用 “独立标准化" 策略:
对每种类型的信号单独计算μ与σ(如振动用μv、σv,温度用μt、σt);
标准化后,若需融合输入模型,可通过 “特征权重分配"(如振动特征权重0.6,温度特征权重 0.4)平衡贡献度。
三、信号标准化应用实例
以 “轴承故障诊断" 为例,完整流程包含“信号采集→预处理→标准化→特征提取→SVM 分类",通过对比 “标准化" 与 “未标准化" 的效果,验证其工程价值。
数据来源:某能源企业轴承故障数据库,包含正常、内圈故障、外圈故障、滚动体故障 4 类信号(采样频率 25.6kHz);
特征提取:经PCA降维后选取8个特征指标分别是:时域(峰值因子、峭度),频域(重心频率、均方频率)、时频域特征(小波包能量熵、瞬时频率标准差),非线性特征(近似熵、样本熵);
模型:SVM(RBF 核,惩罚系数 C=10,核参数 σ=1)。
处理方式 | 特征均值标准差(以峰值因子为例) | 模型分类准确率 | 训练时间 | 误判类型 |
未标准化 | 原始峰值因子范围2.2~8.6,标准差1.9 | 78.3% | 12s | 内圈故障与滚动体故障误判率 25% |
Z-score 标准化 | 标准化后峰值因子范围-1.8~3.2,标准差1.0 | 95.2% | 8s | 误判率降至 4.2%,仅外圈故障偶有误判 |
滑动窗口标准化(非稳态) | 标准化后峰值因子范围-2.2~3.5,标准差1.1 | 96.3% | 10s | 误判率 3.8%,适应转速波动场景 |
标准化使特征的 “区分度提升":峰值因子在故障与正常信号间的差异从原始3.2放大至标准化后的2.8个标准差,SVM更易划分分类边界;
标准化加速模型训练:消除量纲差异后,SVM 的梯度下降收敛速度提升 30%;
标准化增强鲁棒性:对转速波动(±50rpm)的非稳态信号,滑动窗口标准化的准确率比未标准化高 18.1%。
四、结论与展望
数据标准化虽为信号处理中的 “基础步骤",但其技术细节(如统计量计算方式、场景适配策略)直接决定后续分析的精度。核心结论如下:
本质定位:标准化是 “信号物理意义" 与 “模型数学需求" 的桥梁,需在保留信号特征的前提下,实现尺度统一;
关键原则:稳态信号用全局统计量,非稳态信号用滑动窗口统计量,多源信号用独立统计量,避免数据泄露与异常值干扰;
未来方向:随着边缘计算与实时信号处理的发展,轻量化标准化算法(如基于整数运算的近似 Z-score)将成为研究热点,可满足传感器节点的低算力、低延迟需求。
在实际工程中,需避免 “一刀切" 的标准化方式,结合信号类型、工况特点与后续分析目标,制定针对性方案 —— 这既是标准化的技术核心,也是信号处理从 “理论" 走向 “实践" 的关键。